Pseudo Two-dimensional (P2D) Li-Ion Battery Model

As an introductory statement, if the Single Particle Model can be thought of as two single particles, illustrated below:

Then the Pseudo Two-Dimensional model can be thought of as a bunch of these particles, at different depths in the electrode, surrounded by electrolyte.

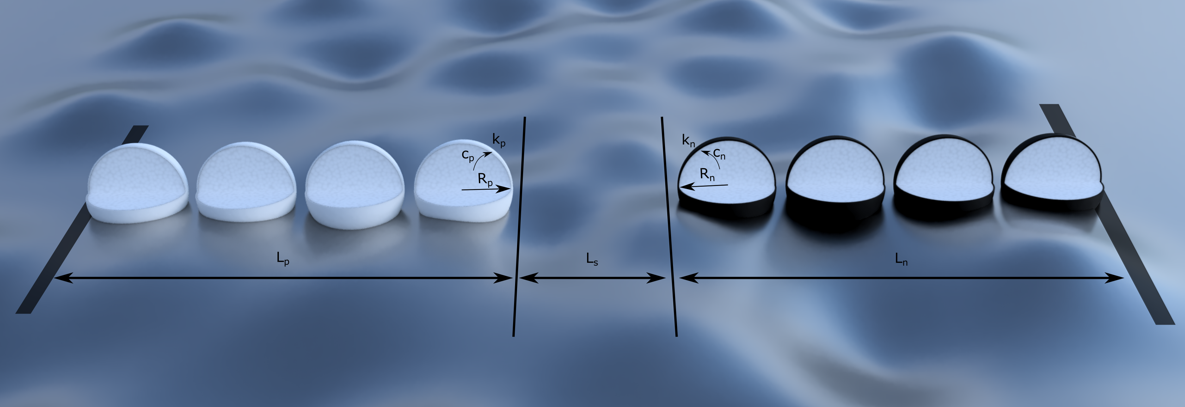
What this means is that the additional complexity compared to the Single Particle Model nets you the following things:

• Increased accuracy related to depth effects (lithium is preferentially selected from the closer electrode material)
• Increased accuracy related to electolyte effects (lithium diffusion through electrolyte can be slow)
• Increased accuracy related to overpotentials at the electrode surface (more accurately captures Solid-Electrolyte Interface growth or Lithium Plating)

Why do we care about Overpotentials?

Overpotentials drive a phenomenon known as Lithium Plating.

Lithium plating is the act of Lithium precipitating out of solution (electrolyte) rather than moving nicely into the electrode material (intercalation). It generally happens when the overpotential, or electrochemical driving force, goes negative at the grapitic electrode. This can happen during charge, especially during fast charge, right at the CC-CV (constant-current, constant-voltage) knee during the charge cycle. In other words, the red line below would cause significantly less degradation than the blue line, despite being otherwise identical.

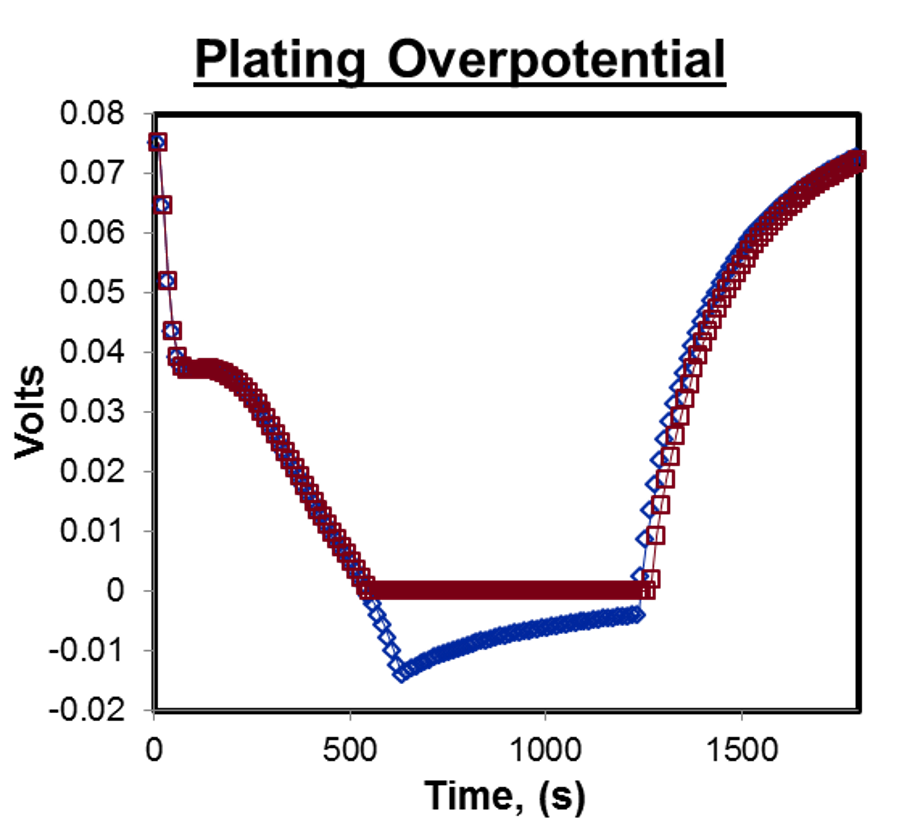
This reaction is irreversible and is one of the main modes of degradation of lithium cells (with the others being related to material stresses caused by swelling during charge / discharge).

How Can A Battery Model Help?

By restricting the overpotential during a charge cycle, a properly-fitted battery model can restrict the charging conditions such that the overpotential at the negative electrode never goes negative, which can greatly extend the lifetime of the battery by preventing the above plating phenomnenon.

The Model

The pseudo-two-dimensional model can be split into a few different mechanisms:

Solid-Phase Mass Transport - Fick's 2nd Law of Diffusion

This equation describes the way that lithium ions diffuse once inside the particles. This is a partial differential equation - the left hand side is the derivative with respect to time, and the right hand side is the derivative with respect to space. This particular formulation captures the spherical nature of the particles.

$\frac{\partial c_{s}}{\partial t} = \frac{D_s}{r^2}\frac{\partial}{\partial r}(r^2 \frac{\partial c_s}{\partial r})$

where concentration $c_s$ has units $\frac{mol}{m^2}$

and Solid-Phase Diffusion rate is $D_s$ has units $[\frac{m^2}{s}]$

and particle radius $r$ has units $m$

For this set of equations, which exist in both the positive and negative particle, we need one initial condition for time and two boundary conditions for space. The initial condition is the initial concentration at all r:
$c_s[0,r] = c_{s, initial}$

Just like the Single Particle Model, boundary conditions are Radial Symmetry (flux = 0) at the center and the ions either enter or leave the surface based on the current $J$:

$\frac{\partial c_s}{\partial r} = 0 @ [t, r=0]$

$\frac{\partial c_s}{\partial r} = \frac{-J}{D_sa_il_i} @ [t, r=R]$

where $J$ is the ionic current, or the rate at which Li ions are entering or leaving the particle, and has units $\frac{mol}{s}$

and $a_i$ is the surface area per unit volume of electrode $i$, which is different for the positive and negative electrodes, and has units $\frac{m^2}{m^3}$

and $l_i$ is the electrode thickness and has units $m$

This set of equations is replicated for each simulated particle, which are treated mathematically as discrete entities whose only interaction is through the varying concentration / potential gradients present in the electrolyte.

Solid-Phase Electonic Conduction

This equation governs the solid-phase potential across the electrodes, which contributes to the behavior as a function of the depth of the electrode.

$\sigma _{eff, i} \frac{\partial ^2 \Phi_1}{\partial x^2} = a_pFj_i$

where $\sigma_{eff, i}$ is the electronic conductivity of the electrode material and has units $\frac{S}{m}$,

and $\Phi_1$ is the solid-phase potential and has units $V$,

and $x$ is the distance across the cell and has units $m$,

and $a_i$ is the surface area per unit volume of electrode $i$, which is different for the positive and negative electrodes, and has units $\frac{m^2}{m^3}$,

and $j_i$ is the anodic or cathodic current density and has units $\frac{mol}{m^2s}$,

and $F$ is Faraday's Constant and is approximately $96485 \frac{C}{mol}$.

Electrolyte Charge Balance

This equation governs liquid potential, which also contributes to the behavior as a function of electrode depth.

$-\sigma _{eff, i} \frac{\partial \Phi_1}{\partial x} -\kappa_{eff, i} \frac{\partial \Phi_2}{\partial x} + \frac{2 \kappa_{eff, i}RT}{F}(1-t_+)\frac{\partial \ln c_e}{\partial x} = I$

where $\sigma_{eff, i}$ is the electronic conductivity of the electrode material and has units $\frac{S}{m}$,

and $\Phi_1$ is the solid-phase potential and has units $V$,

and $\Phi_2$ is the liquid phase potential and has units $V$

and $x$ is the distance across the cell and has units $m$,

and $\kappa _{eff, i}$ is the effective reaction rate and has units $\frac{m^{2.5}}{mol^{0.5}s}$,

and $F$ is Faraday's Constant and is approximately $96485 \frac{C}{mol}$,

and $R$ is the Universal Gas Constant and is approximately $8.3145 \frac{J}{mol K}$,

and $t_+$ is the Transference Number, which for Lithium is approximately $0.363$,

and $T$ is the temperature, which has units $K$,

and $c_e$ is the electrolyte concentration and has units $\frac{mol}{m^3}$. In this model, this concentration changes. When electrolite Li diffusion is slow, it can be the limiting factor in cell performance.

Electrolyte Material Balance (back to Fick's Law)

This equation governs the Li transport in the electrolyte phase, which tracks how Li particles move from cathode to anode and vice-versa.

$-\epsilon _{i} \frac{\partial c_e}{\partial x} = -D_{eff, i} \frac{\partial ^2 c_e}{\partial x^2} + a_i(1-t_+)j_i$

where $\epsilon_i$ is the volume fraction of that region (positive, separator, negative) that is electrolyte and has units $\frac{m^3}{m^3}$,

and $c_e$ is the electrolyte concentration and has units $\frac{mol}{m^3}$

and $x$ is the distance across the cell and has units $m$,

and $D_{eff, i}$ is the effective diffusion rate for that region and has units $\frac{cm^2}{s}$,

and $a_i$ is the electrode area per unit volume in that region (positive, negative) and has units $\frac{m^2}{m^3}$,

and $t_+$ is the Transference Number, which for Lithium is approximately $0.363$,

and $j_i$ is the anodic or cathodic current density and has units $\frac{mol}{m^2s}$.

Other expressions

Effective Reaction Rate

This expression describes the relative reaction rate based on pore tortuosity

$\kappa _{eff,i} = \epsilon_i^{brugg_I}\kappa_i$

where $\kappa_i$ is the given reaction rate in that region (positive, negative) and has units $\frac{m^{2.5}}{mol^{0.5}s}$

and $brugg_i$ is the bruggman coefficient - it captures the tortuosity associated with the pores in the electrode and is unitless.

and $\epsilon_i$ is the volume fraction of that region (positive, separator, negative) that is electrolyte and has units $\frac{m^3}{m^3}$

Butler-Volmer Kinetics at Each Electrode

The current is dictated by Butler-Volmer kinetics, which relate the potential and reaction rate to the current. This can be thought of as one element of a battery's 'resistance' - in order to move electrons, there has to be a voltage drop. This really describes how the amount of current that flows relates to the difference between the external voltage and the battery's Open Circuit Potential (U). The Open Circuit Potential is what gives a battery discharge curve its shape and really dictates the voltage window of the battery.

Above, the total current $j$ is described in terms of the sum of the anode current $j_a$ and the cathode current $j_c$. This equation captures the nonlinear relationship between a voltage perturbation and the resulting battery current.

$j_i = 2\kappa_{eff,i}(c_{s, max,i}-c^s_i)^{0.5}c^{s0.5}_ic^{0.5}sinh(\frac{0.5F}{RT}(\eta_i))$

$\eta_i = \Phi_1-\Phi_2-U_i$

where $j_i$ is the anodic or cathodic current density and has units $\frac{mol}{m^2s}$,

and $k_{eff,i}$ is the effective reaction rate for that electrode and has units $\frac{m^{2.5}}{mol^{0.5}s}$

and $c_{i}$ is the lithium concentration at the particle surface and has units $\frac{mol}{m^3}$,

and $c_{s,max,i}$ is the solid maximum lithium concentration and has units $\frac{mol}{m^3}$,

and $F$ is Faraday's Constant and is approximately $96485 \frac{C}{mol}$,

and $R$ is the Universal Gas Constant and is approximately $8.3145 \frac{J}{mol K}$,

and $T$ is the temperature, which has units $K$,

and $c_e$ is the electrolyte concentration and has units $\frac{mol}{m^3}$.

$sinh(x)$ is a practical approximation to $0.5 * e^{+ix} - e^{-ix}$

$U_i$ is a fitted relationship between the open-circuit potential and the degree of lithiation of each electrode

• this is a material property that is generally measured experimentally.

The Path of A Lithium Particle

During charge, the lithium begins in the anode. An external voltage is applied, and this splits the electron off of the Lithium. The electron is removed from the system by way of electronic conduction through the graphite structure to the current collector, and the Li+ diffuses out of the porous electrode. These relationships are captured by the Fick's Law equation, the Electronic Conduction, the Charge Balance, and the Butler-Volmer Kinetic equations.

As the Li+ is generated at the anode and diffuses into the electrolyte, the charge balance of the system changes. These mechanics are captured in the Charge Balance equation, which relies on $c$, the concentration of lithium in the electrolyte, $\kappa_{eff}$, the effective rate of reaction, and $\sigma_{eff}$, the electronic conductivity of the material. Together, this equation couples the diffusion, reaction rate, and electronic conduction equations in order to accurately capture the driving force behind the charge at different points in the electrode.

Once the lithium ion leaves the anode particle, it diffuses through the separator in the electrolyte.

When it reaches the cathode, it is free to combine with another electron and this process happens in reverse - the varying potentials in the solid material and liquid electrolyte drive the local reactions, where Lithium intercalates into the cathodic crystal structure.

Implementation

For the model (as implemented in Ampere) the following parameters are available:

name	description	default value	Units
D1	Li+ Diffusivity in electrolyte	0.15e-8	$cm^2/s$
Dp	Li+ Diffusivity in positive particle	7.2e-14	$cm^2/s$
Dn	Li+ Diffusivity in negative particle	7.5e-14	$cm^2/s$
cspmax	Maximum Li concentration of positive solid	45829	$mol/m^3$
csnmax	Maximum Li concentration of negative solid	30555	$mol/m^3$
ls	Separator thickness	16e-6	$m$
lp	Positive electrode thickness	43e-6	$m$
ln	Negative electrode thickness	46.5e-6	$m$
es	Separator volume fraction of pores	0.45	$m^3/m^3$
ep	Positive electrode volume fraction of pores	0.4	$m^3/m^3$
en	Negative electrode volume fraction of pores	0.38	$m^3/m^3$
efn	Negative electrode filler fraction	0.0326	$m^3/m^3$
efp	Positive electrode filler fraction	0.025	$m^3/m^3$
brugs	Separator Bruggeman coefficient - pore tortuosity	1.5
brugn	Negative electrode Bruggeman coefficient - pore tortuosity	1.5
brugp	Positive electrode coefficient - pore tortuosity	1.5
sigma_n	Negative electrode electrical conductivity	100	$S/m$
sigma_p	Positive electrode electrical conductivity	10	$S/m$
t+	Transference Number - fraction of ionic current carried by Li+	0.363
Rp	Positive particle radius	10e-6	$m$
Rn	Negative particle radius	8e-6	$m$
T	Ambient Temperature	303.15	$K$
ce	Starting electrolyte Li+ concentration	1200	$mol/m^3$
ap	Surface area of positive electrode per volume	885000	$m^2/m^3$
an	Surface area of negative electrode per volume	723600	$m^2/m^3$
kp	Positive electrode reaction rate	0.10307e-9	$m^2.5/(mol^0.5s)$
kn	Negative electrode reaction rate	0.1334e-9	$m^2.5/(mol^0.5s)$
N1	Positive electrode number of FD Nodes	7
N2	Separator number of FD Nodes	3
N3	Negative electrode number of FD Nodes	7
Nr1	Positive particle number of FD nodes (per particle)	3
Nr2	Negative particle number of FD nodes (per particle)	3