Single Particle Li-Ion Battery Model (SPM)

An interactive form of the model is available here

The Single Particle Model (SPM) is a relatively sophisticated physics-based lithium ion battery model.
It incorporates Fick's Law of Diffusion and Butler-Volmer kinetics, but does not include any electrolyte effects, electrode depth effects, or electrode porosity effects, which can limit the applicability in real-world scenarios. Specifically, it is at its most valid during low charge / discharge rates.

Below is a representation of a typical cell - it has a cathode, a separator, and an anode. The cathode and anode regions are the ones relevant to this model, which are where lithium is accrued during discharge and charge, respectively.

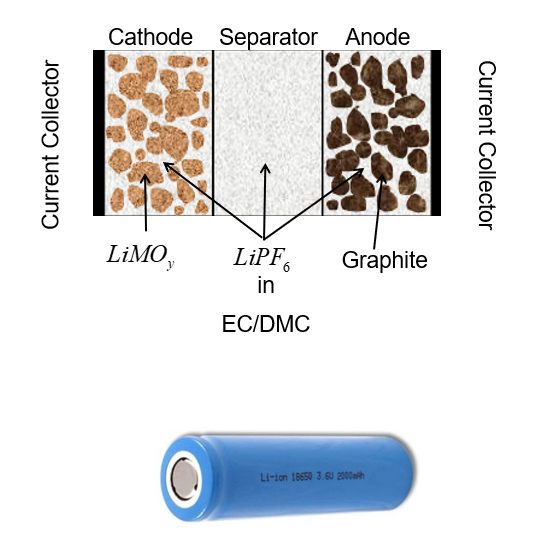
In practical terms, during charge, a lithium ion de-intercalates from the cathode and, upon leaving the surface of the positive electrode particle, is transported to an infinite pool of electrolyte, from where it intercalates into the negative electrode particle and is stored internally. The concentrations in both the positive and negative electrodes are tracked and the surface area is calculated based upon the assumed particle radius, electrode thickness, and active area per unit volume. The particles are all assumed to be perfect spheres of uniform size, meaning the entire electrode can be represented as a single particle, where the current density at the surface is simply scaled to the expected area of an entire cell.

The model can be split into a few different mechanisms:

Mass Transport - Fick's 2nd Law of Diffusion

$\frac{\partial c_{s}}{\partial t} = \frac{D_s}{r^2}\frac{\partial}{\partial r}(r^2 \frac{\partial c_s}{\partial r})$

where concentration $c_s$ has units $[\frac{mol}{m^2}]$

and Solid-Phase Diffusion rate is $D_s$ has units $[\frac{m^2}{s}]$

and particle radius $r$ has units $m$

This equation describes the way that lithium ions diffuse once inside the particles. This is a partial differential equation - the left hand side is the derivative with respect to time, and the right hand side is the derivative with respect to space.
This particular formulation captures the spherical nature of the particles.

For this set of equations, which exist in both the positive and negative particle, we need one initial condition for time and two boundary conditions for space. The initial condition is the initial concentration at all r, which is set independently for positive and negative particles:
$c_s[0,r] = c_{s, initial}$

The boundary conditions are Radial Symmetry (flux = 0) at the center and the ions either enter or leave the surface based on the current $J$:

$\frac{\partial c_s}{\partial r} = 0 @ [t, r=0]$

$\frac{\partial c_s}{\partial r} = \frac{-J}{D_sa_il_i} @ [t, r=R]$

where $J$ is the ionic current, or the rate at which Li ions are entering or leaving the particle, and has units $\frac{mol}{s}$

and $a_i$ is the surface area per unit volume of electrode $i$, which is different for the positive and negative electrodes, and has units $\frac{m^2}{m^3}$

and $l_i$ is the electrode thickness and has units $m$

The current is dictated by Butler-Volmer kinetics, which relate the potential and reaction rate to the current.
This can be thought of as one element of a battery's 'resistance' - in order to move electrons, there has to be a voltage drop. This really describes how the amount of current that flows relates to the difference between the external voltage and the battery's Open Circuit Potential (U). The Open Circuit Potential is what gives a battery discharge curve its shape and really dictates the voltage window of the battery.

Above, the total current $j$ is described in terms of the sum of the anode current $j_a$ and the cathode current $j_c$. This equation captures the nonlinear relationship between a voltage perturbation and the resulting battery current.

$j_i = k_i c_{s,max,i}c_e^{0.5}{e}(1-x_{surf, i})^{0.5}x_{surf, i}^{0.5}[exp(\frac{0.5 F}{RT}\eta_i)-exp(-\frac{0.5 F}{RT}\eta_i)]$

$\eta_i = \phi(x_{surf})_i-U_i$

where $j_i$ is the anodic or cathodic current density and has units $\frac{mol}{m^2s}$,

and $k_i$ is the reaction rate for that electrode and has units $\frac{m^4}(mol s)$,

and $x_{i, surf}$ is the lithiation fraction of the particle surface and has units $\frac{mol/m^3}{mol/m^3}$,

and $c_{s,max,i}$ is the solid maximum lithium concentration and has units $\frac{mol}{m^3}$,

and $c_e$ is the electrolyte concentration and has units $\frac{mol}{m^3}$. It is set once and never changes as a core assumption of this model.

For the model (as implemented in Ampere), the following parameters are available:

name	description	default value	Units
Dn	Li+ Diffusivity in negative particle	3.9e-14	m^2/s
Dp	Li+ Diffusivity in positive particle	1e-14	m^2/s
Rn	Negative particle radius	2e-6	m
Rp	Positive particle radius	2e-6	m
T	Ambient Temperature	303.15	K
an	Surface area per unit volume of negative electrode	723600	m^2/m^3
ap	Surface area per unit volume of positive electrode	885000	m^2/m^3
ce	Starting electrolyte Li+ concentration	1000	mol/m^3
csnmax	Maximum Li+ concentration of negative solid	30555	mol/m^3
cspmax	Maximum Li+ concentration of positive solid	51555	mol/m^3
kn	Negative electrode reaction rate	5.0307e-9	m^4/mol s
kp	Positive electrode reaction rate	2.334e-9	m^4/mol s
ln	Negative electrode thickness	88e-6	m
lp	Positive electrode thickness	80e-6	m